In this blog post I’ll talk about the theoretical background and the technical implementation of cola, a text CRDT for real-time collaborative editing written in Rust. Reading this is not at all necessary to be able to use cola, so if that’s all you’re interested in you can safely skip this post and go straight to the documentation.
The post is divided into three parts:
-
in the first part we’ll go over how to represent the state of the document and the edits that transform it in a way that guarantees convergence across all replicas. The ideas presented in this part are widely covered in the literature, so if you’re already familiar with text CRDTs you can probably skip it;
-
in the second part we’ll see how to efficiently implement the framework discussed in the first part in code;
-
finally, in the third part we’ll look at some benchmarks comparing cola to other Rust-based CRDT libraries.
First part: Intro to text CRDTs
A Conflict-free Replicated Data Type, or CRDT, is an umbrella term for any data structure that can be replicated and modified concurrently across multiple sites, and is guaranteed to converge without the need for a central authority to coordinate the changes.
There are many different kinds of CRDTs: counters, sets, maps, lists, trees, etc. Here we’ll focus on a sequence CRDT that can be used to represent plain text documents.
In the setting of our problem we have a number of peers on a distributed network all editing the same document. Each peer can insert or delete text and immediately see the changes applied to their local replica. These edits are then sent to the other peers which somehow integrate them into their own replicas.
The only assumption we make on the network layer is that every edit is received by all the peers in the network. Edits can be sent multiple times and in any order, but they must eventually reach all the peers.
Our goal is to design a data structure that can, at the very minimum, converge to the same state at every peer once all the edits have been received. The final document we end up with should also “make sense” from the user’s point of view. For example, we could have a CRDT that sorts the inserted characters in alphabetical order. This would technically solve all concurrency problems, but I doubt anyone would use it.
Anchors in a sea of text
Let’s start by looking at the simplest approach: doing nothing. When someone
inserts or deletes some text we just broadcast the edit “as is”: insert "abc" at offset 8, delete between offset 10 and offset 13, etc.
This is clearly wrong because all we need to diverge is for another peer to
concurrently modify the document in the 0..offset region.
The problem is that offsets depend on the state of the document at the time an edit was made. We can’t just exchange offsets without also exchanging the context they depend on.
What if we used characters to refer to positions in the document instead of
offsets? We could then send insert "abc" after the 'd' or delete between the 'f' and the 'o'.
When a peer receives that edit it doesn’t matter where the 'd' ended up,
they’ll know they have to insert "abc" after it.
But what if there are multiple 'd's in the document? What if the 'd' was
deleted? We still have to think some things through, but the idea of using
content to refer to positions is a step in the right direction.
Let’s solve the first problem: how do we tell our 'd's apart?
In our universe time only flows in one direction, so we could assign an increasing number to each character as it’s inserted into the document. The first character a peer inserts gets the number 0, the second 1, and so on. Timestamping in this way works because for every n, a peer can only insert its n-th character once, so we can use this number as a stable identifier for a position in the document.
Or can we? After all there could many n-th characters in the same document, one
for every peer that ever contributed to it. To distiguish them we also assign
each peer a unique identifier, called a ReplicaId in cola, and
use the pair ReplicaId.n to uniquely identify a character.
Guaranteeing uniqueness of the n half is both possible and easy: we just
increment a local counter. Doing the same for the ReplicaId half without a
central server is not. The best we can do is to use random integers big enough
to make the probability of a collision negligible, like a
UUID.
This n number is also called a temporal offset in cola, and the ReplicaId.n
pair is called an Anchor. Anchors are incredibly important
because they allow us to specify both insertions and deletions in a
concurrency-enabled way. Insertions are identified by a single Anchor which
tells us where to insert the text, while deletions are identified by two
Anchors, one for the start and one for the end of the deleted region.
Breaking ties
When a peer integrates an insertion it may find other insertions in its replica
that have the same Anchor. How do we decide which one comes first?
Intuitively we’d want the last insertion to come first.
But the concept of a “last” operation is not well defined in a distributed system. Using wall clock timestamps is problematic because wall clocks lack monotonicity and also suffer from clock drift. What we really want is a way to determine if an insertion was made in an environment in which another insertion was already present.
This is exactly what Lamport timestamps are used for. A Lamport
clock is a logical clock that is updated by a very simple algorithm: every time
a peer inserts some text it increases its clock by one, and when it receives a
remote insertion it sets the clock to max(current, remote_timestamp) + 1.
This guarantees that if insertion A is made by a peer that has already
integrated insertion B, then A’s Lamport timestamp will be greater than
B’s.
We can now handle conflicting insertions by sorting them in descending order by their Lamport timestamp.
There’s one last case we need to handle: conflicting and concurrent
insertions, i.e. insertions with the same Anchor and Lamport timestamp.
From the user’s point of view there’s not an order that’s more “correct” than
the others, so all we care about is consistency between peers. cola breaks the
tie by sorting in ascending order on the ReplicaId of the peer that made the
insertion.
Deletions
With insertions out of the way let’s now focus on deletions. As I’ve briefly
mentioned, every time a peer deletes some text we transform the start and end
offsets representing the deleted range into Anchors, which we can broadcast
to the other peers.
Deletions are a bit easier to reason about because, unlike with insertions, we don’t have to worry as much about concurrency or causality issues. Two peers concurrently deleting the same region of text produces the same result as if only one of them had done it1: the text is gone.
There are however three problems we need to tackle before we can consider deletions solved:
-
what do we do with the deleted regions of text? We can’t entirely remove them from the document because there may be edits we haven’t yet seen whose
Anchors lie within them; -
how do we know when a remote deletion is ready to be integrated? We’ll diverge if a peer integrates a deletion before it has received all the content that the peer who created the deletion had when they made it;
-
within the region of text included between the start and end
Anchors of a deletion, how do we determine which characters should be deleted and which should be kept? We’ll diverge if the peer who integrates a deletion deletes text that wasn’t yet received by the peer who created the deletion.
The solution to the first problem is to use tombstones. A tombstoned character is simply marked as deleted, but it’s still kept in the document. This clearly increases the memory footprint of our data structure as more and more text is deleted. We’ll see in the performance section how we can mitigate this problem.
A solution to other two problems is to include in the deletion message a map
where the keys are ReplicaIds and the values are the timestamps of the last
character that the peer who created the deletion had seen when they made it.
This is called a version vector2. Version vectors are useful because we can implement a partial order on them that lets us compare what content different peers have seen. If peer A’s vv is >= than peer B’s vv then we know that A has seen at least as much content as B, and possibly more.
Using version vectors we can solve the second problem by making a peer wait to integrate a deletion until its vv is >= than the vv included in the deletion message.
We can also solve the third problem by skipping over characters whose timestamp is strictly greater than the timestamp included in the deletion’s vv.
Second part: cola’s implementation
In the previous part we’ve walked through the theoretical framework cola uses to solve collaborative editing. It’s now time for the fun part: implementing it in code in a performant way.
Linkin Blocks
Let’s start by designing the data structure each peer will use to represent the
state of its local replica of the document. This is called a
Replica in cola.
As we’ve seen, every time a peer inserts some text we assign each character its own block, which includes a temporal offset and a Lamport timestamp. It’s very natural to represent this sequence of blocks as a linked list, so that’s where we’ll start.
Before we dive further into the implementation I’d like to point out something. Up until now I’ve been including the textual content associated with each block in every illustration. This was mostly done for clarity, but none of the algorithms we’ve discussed so far actually need to know what the content of an insertion is.
This also means we can decouple all the CRDT machinery we’re building from the implementation of the text buffer itself. In fact, there’s not a single function in cola’s API that takes a string as an argument. cola has no idea what the content of the document you’re editing is, all it deals with are blocks of numbers.
RLE all the things
The first big optimization we can do is to reduce the number of blocks we need to represent the document. We can’t have any hope of landing on a performant implementation if we have a bunch of metadata associated with every single character that’s ever been inserted.
Luckily, we don’t have to. Every time there’s a run of blocks whose character timestamps increase sequentially we can run-length encode them into a single block. This means pasting the entire Wikipedia page on the Manhattan Project will only take up a single block instead of 107,000.
RLEing in this way also allows us to represent a sentence typed character-by-character without moving the cursor or deleting anything with a single block, instead of one per key press.
These runs of consecutive blocks are called EditRuns in cola.
Once an EditRun is broken it remains fixed for the remaning lifetime of the
document and can’t be extended anymore. A run that’s not yet broken is called
active.
When text is inserted in the midle of an existing EditRun we simply split it
into two shorter runs and insert the new text between them.
When text is removed from the document we split it off from the run it’s part of and mark it as deleted (tombstones, remember?). Deleted runs can also be RLEd in the same way as active runs, which mitigates the memory footprint problem we mentioned in the previous section.
A better alternative: B-trees
There’s two distinct paths we need to think about while designing our data structure:
-
the upstream path, which deals with transforming a local edit specified in terms of offsets into the document into an edit that can be sent to other peers, and
-
the downstream path, which deals with transforming a remote edit received from another peer into a local edit that can be applied to the document.
Let’s start by improving the upstream path. For both insertions and deletions this boils down to:
-
finding the run that contains an offset to create an
Anchor; -
if necessary, splitting it into a max of two (for insertions) or three (for deletions) smaller runs.
Since we’re using a linked list the second step is O(1). The first one
however requires us to scan the entire list from the beginning of the document
until we land on the right run, which is a linear time complexity. Not good.
We could improve this by caching a pointer to the currently active run together with the run’s offset in the document. This helps because when we edit a document we don’t jump around randomly. We usually insert or delete entire runs of characters before moving the cursor. There are editing patterns that don’t follow this assumption like when using multiple cursors, but it’s still a good heuristic.
While this makes the best-case performance constant, the worst case would still be linear. If the user inserts a character at the start of the document and then another one at the end we still have to walk the entire list.
It’s clear that a linear data structure won’t cut it if we want to be performant with all kinds of editing patterns. We need a logarithmic worst-case complexity.
This is where B-trees come in. A B-tree is a balanced tree where every node can have a variable number of children between a minimum and a maximum. “Balanced” simply means that for every internal node, all its children have the same height.
The runs that where previously the nodes of the linked list are now represented as leaves in the B-tree. Leaves are grouped into internal nodes, or inodes for short. Each inode stores not only its children but also the sum of their lengths (with tombstoned runs contributing a length of 0). Inodes are in turn grouped into other inodes all the way up to the root, whose length coincides with the length of the document.
B-trees are a great fit for our problem because they can be traversed and inserted into in logarithmic time.
To reach a given run we start from the root and loop through its children until we find the one containing the offset we’re looking for. We then simply repeat the same process with the child until we reach a leaf node.
Inserting a new run is in general a bit more involved because we need to make
sure that the tree remains balanced and that all its other invariants are
preserved. I won’t go into the details here, but the important thing is that
this can be done in O(log n).
By using a B-tree we can do local edits in logarithmic time. Great! But what
about integrating remote edits? If we receive an edit like insert 2.3..7 at 1.2 we currently have no way to efficiently find the run that contains the
anchor 1.2. We’d have to check every single run from the beginning of the
document until we find the right one.
An even better alternative: G-trees
The problem with our B-tree is that we don’t have a way to identify its
leaves, and if we can’t identify them we can’t efficiently perform the
anchor -> run conversion.
We could store pointers to the leaves somewhere, but what do we use them for? Having a pointer to the leaf of a B-tree doesn’t really help because insertions are performed top-down, starting from the root, and a pointer doesn’t tell us how to “navigate” down the tree to reach the leaf it points to.
Well, then “just do them bottom-up!” you might say. This would require to store
a parent pointer in every node of the tree (except the root), effectively
creating a sort of “doubly-linked” B-tree. Also remember that cola is written
in Rust, and the Rust compiler really doesn’t like data structures that don’t
have a clear ownership hierarchy. If you tried to implement this in safe Rust
you’d quickly end up with with a bunch of Rc<RefCell<_>>s everywhere, which
is not only slow but also ugly.
By wondering into the unsafe lands of Rust we could probably do it with raw
pointers and Pinned nodes, but to prove that that kind of code is safe I’d
have to reason a lot more about how computers actually work than I’d like to. I
like Rust because it allows me not to do that.
The ownership model of a B-tree is very simple: every inode owns its children. Unfortunately this simplicity leads to the kinds of problems I’ve described if we want to do bottom-up operations. What we need is a way to express which children belong to which parent, without having the latter actually own them (in the Rust sense of the term).
The solution is surprisingly simple: we can store every node in a dynamic
array, (a Vec in Rust) and use indices into this vector to refer to other
nodes. This solves the ownership problem because the vector now owns all the
nodes. And by simply storing the index of the parent in every node we can
navigate the tree in both directions without having to use any unsafe code.
This all hinges on the assumption that once we’ve inserted a node into the vector its index never changes. Inserting new nodes doesn’t cause any issues: we just append them to the end. Removing a node however would be doubly bad: not only is it a linear operation (because we’re now using a vector instead of a tree), but it would also invalidate all the indices of the nodes that come after it.
But as we’ve seen we never remove runs from the document anyway. Deleting some text only marks the corresponding run as tombstoned, but it’s still there, so we don’t have to worry about this.
I couldn’t find any established name for this kind of tree-in-a-vector data structure, so I’ve been calling it a G-tree, short for grow-only tree.
The Rust code for it is slightly more efficient than what I’m presenting here, but it’s basically:
trait Leaf (
fn len(&self) -> u64;
)
struct Gtree<L: Leaf> (
inodes: Vec<Inode>,
leaves: Vec<Leaf<L>>,
root_idx: InodeIdx,
)
struct Inode {
children: Vec<NodeIdx>,
parent: Option<InodeIdx>,
total_len: u64,
}
struct Leaf<L> {
value: L,
parent: InodeIdx,
}
enum NodeIdx {
Inode(InodeIdx),
Leaf(LeafIdx),
}
struct InodeIdx(usize);
struct LeafIdx(usize);
The nice properties of the B-tree that we care about, namely top-down search and insertion in logarithmic time, are still here. This is because we still have the structure of a B-tree, i.e. the parent-child relationships between the nodes, we’ve just changed its representation in memory.
But this is not all. By using a G-tree we get a few other nice properties for free:
-
we can use the index of a leaf in the vector – a.k.a. the
LeafIdx– as a stable identifier for that leaf. No pointers, yay! -
remember when we considered caching the pointer to the currently active run when we were trying to make the linked-list-based implementation faster? We can do that now, except instead of storing a pointer we store the
LeafIdxof the run.This is a big deal because it makes repeated edits at the same cursor location extremely fast. We just extend the active run and update the length of every ancestor all the way up to the root.
Let’s do a bit of math to estimate just how (in)expensive cursor-cache hits are. cola’s G-tree has a branching factor of 32, with an average occupancy of around 20 children per inode3. With just 4 levels we usually store around 160k distinct
EditRuns, and even documents with very long editing histories barely reach a fraction of that4.This means a cache hit costs us a few integer comparisons and 2-4 integer additions. No tree traversals and no new allocations. It doesn’t get much faster than that;
-
serializing and deserializing becomes trivial. (De)Serializing things that are represented as trees in memory is always a bit annoying because it involves “flattening” the tree into a linear sequence of bytes in a way that preserves its structure. But in a G-tree everything is already stored linearly in memory, so we can just (de)serialize the vector.
Anchors to Leaves
Let’s recap our performance journey so far:
-
we started with a linked list of runs, which was slow (linear) for both upstream and downstream operations;
-
we then switched to a B-tree, which was logarithmic for upstream operations but still still linear for downstream ones;
-
we’ve finally landed on the G-tree which, like the B-tree, is logarithmic for upstream operations, but can also be logarithmic for downstream ones.
Remember that downstream operations involve integrating remote edits of the
form insert 2.3..7 at 1.2 or delete between 3.4 and 2.2. All the operations
are specified in terms of anchors. To turn them into concrete edits the user
can apply we need to convert the anchors into offsets into the document, i.e.
turning them into something of the form insert 2.3..7 at 18 or delete between 17 and 25.
We’ve also seen how the G-tree can be traversed in both directions, so if we
knew which run contains a given anchor we could easily get the corresponding
offset by traversing the tree upwards. And “knowing which run” really means
“knowing which LeafIdx”, because as we’ve seen the LeafIdx acts as a stable
identifier for a run.
We’ve reduced the problem of integrating remote edits into performing the
Anchor -> LeafIdx conversion. But this is relatively easy compared to what
we’ve done so far.
A simple solution would be to keep a secondary G-tree (or even a B-tree) where
the leaves contain the ReplicaId, the temporal range and the LeafIdx of the
run containing the same ReplicaId and range in the main G-tree, like so:
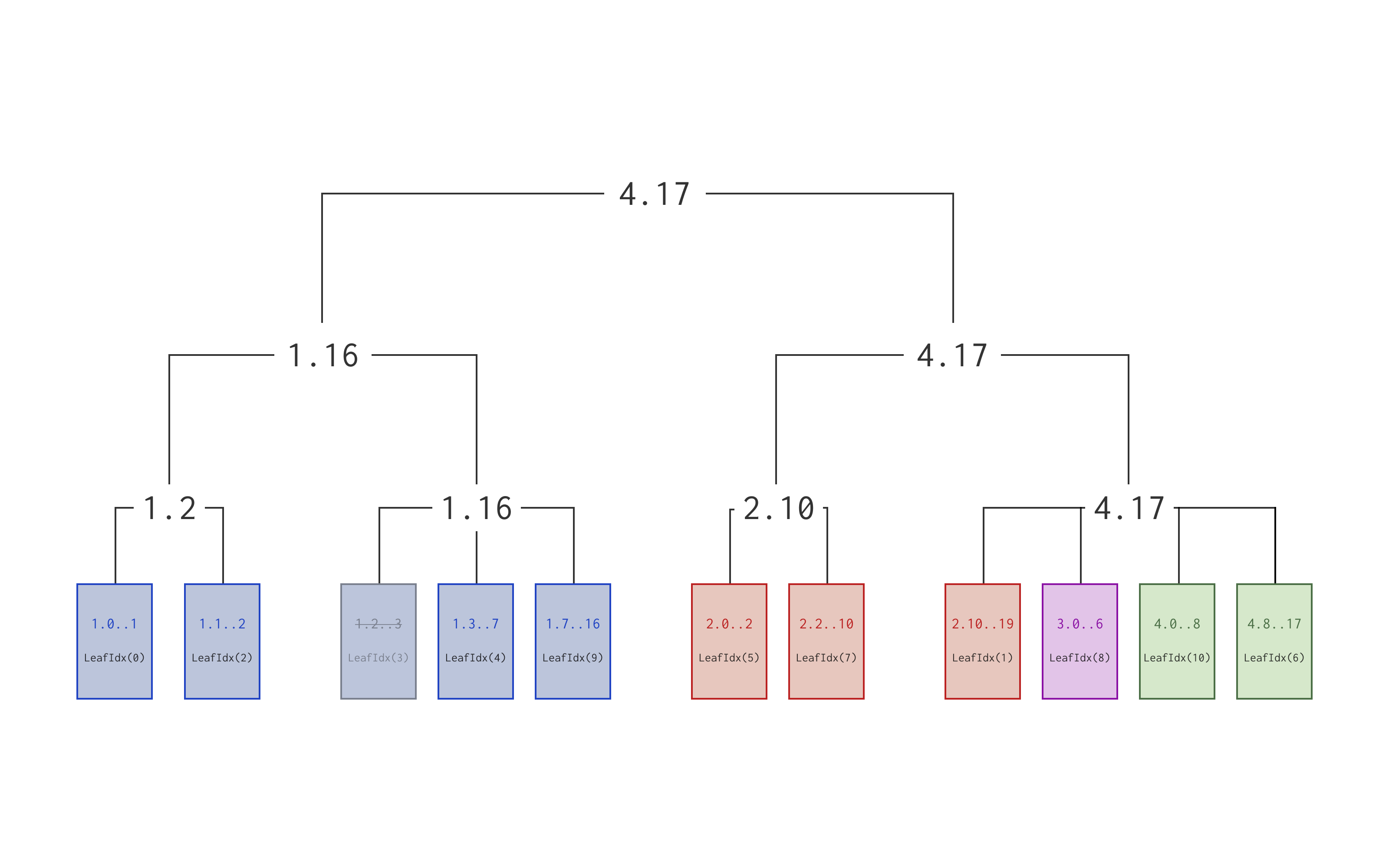
Note how the leaves of this tree are totally ordered, first by ReplicaId and
then by temporal range. A total order allows us to bubble the greatest
Anchor within the children of an inode up to the root, and use Anchors
as offsets into this tree. When we need to convert an Anchor into a LeafIdx
we just navigate the tree downwards until we find the right leaf, which will
contain the LeafIdx we’re looking for.
This is a perfectly valid design since search and insertion both run in O(log n), where n is the total number of runs in the document, which is the same
complexity as the main G-tree.
With that said, you won’t find this secondary G-tree in cola’s source code. I
won’t go over the details of the actual implementation cola uses because it’s a
bit involved and there’s not a ton to learn from it. The important thing to
know is that both search and insertion are O(log f), where f is the number
of “fragments” that the EditRun containing the anchor has been split into
over time. Of course f is always <= than n, and usually much smaller than
it.
Aaand.. we’re done! We’ve finally reached a design that guarantees convergence, intent preservation and good performance (we’ll see just how good in the following (and final) section).
There’s actually still work to do to make cola production-ready like supporting undo/redo and a few other things, but the foundation is there.
Third part: Benchmarks
I’ve benchmarked cola against 3 other CRDTs implemented in Rust: diamond-types, automerge and yrs. I’ve measured the time each CRDT takes to process the editing history of a real-world character-by-character editing trace taken from this dataset using criterion, a popular benchmarking library for Rust. Each trace was measured in both the upstream and downstream directions. This is the code that’s being benchmarked.
In the following graphs I’m using cola’s performance times 100 as the deadline, so if a CRDT is more than 100x slower than cola its measurement is not shown.
The benchmarks were run on a 2018 MacBook Pro with a 2.2 GHz 6-Core Intel Core i7. If you run them on your machine you’ll probably get different results, but the relative performance of the CRDTs should be similar.
In the upstream direction both yrs and automerge go over the deadline, with cola being 1.4-2x faster than diamond-types.
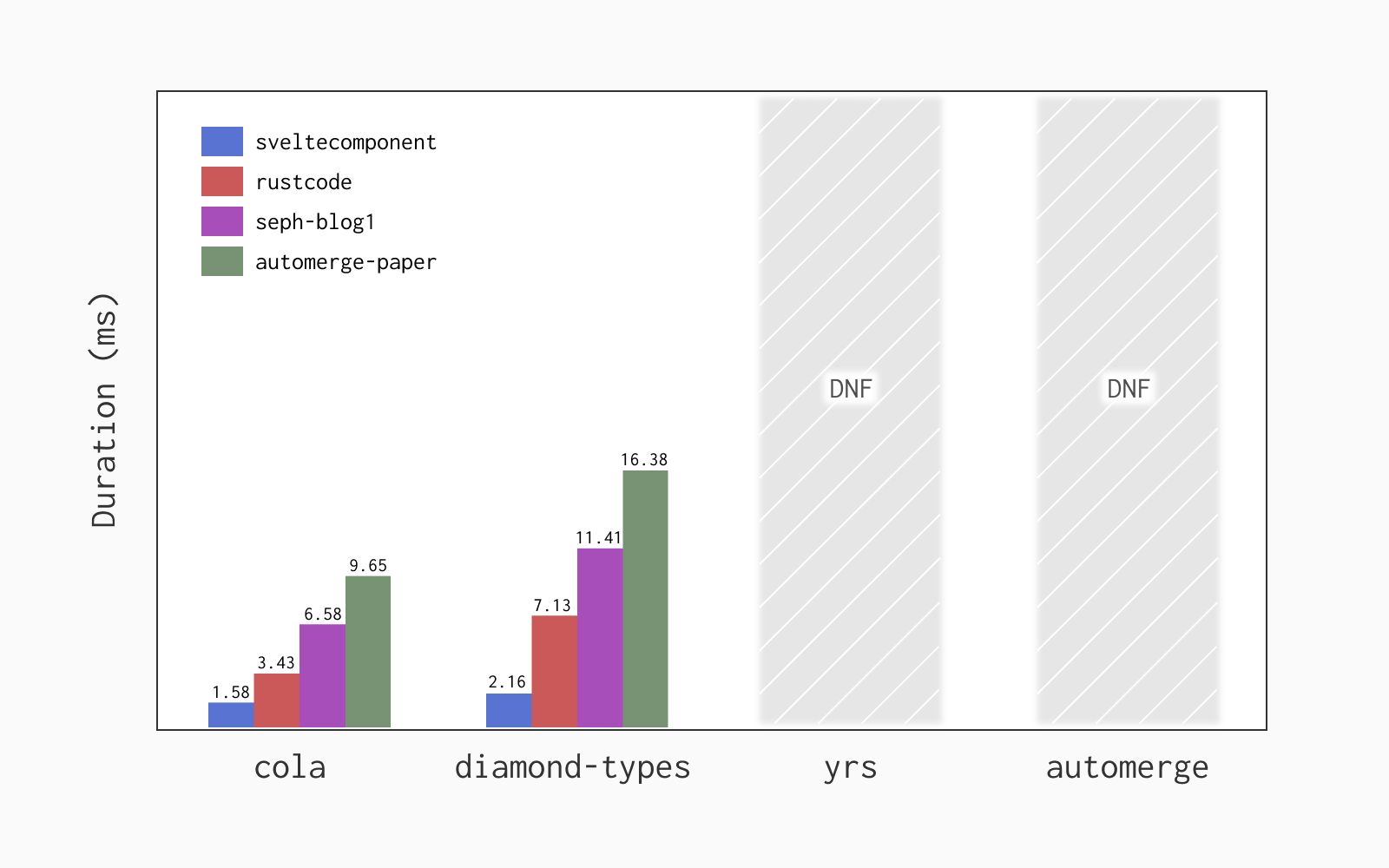
The results in the downstream direction are similar, except now diamond-types crashes with every trace so I couldn’t get any measurements (if it was my fault for not using the library correctly please let me know and I’ll update the post).
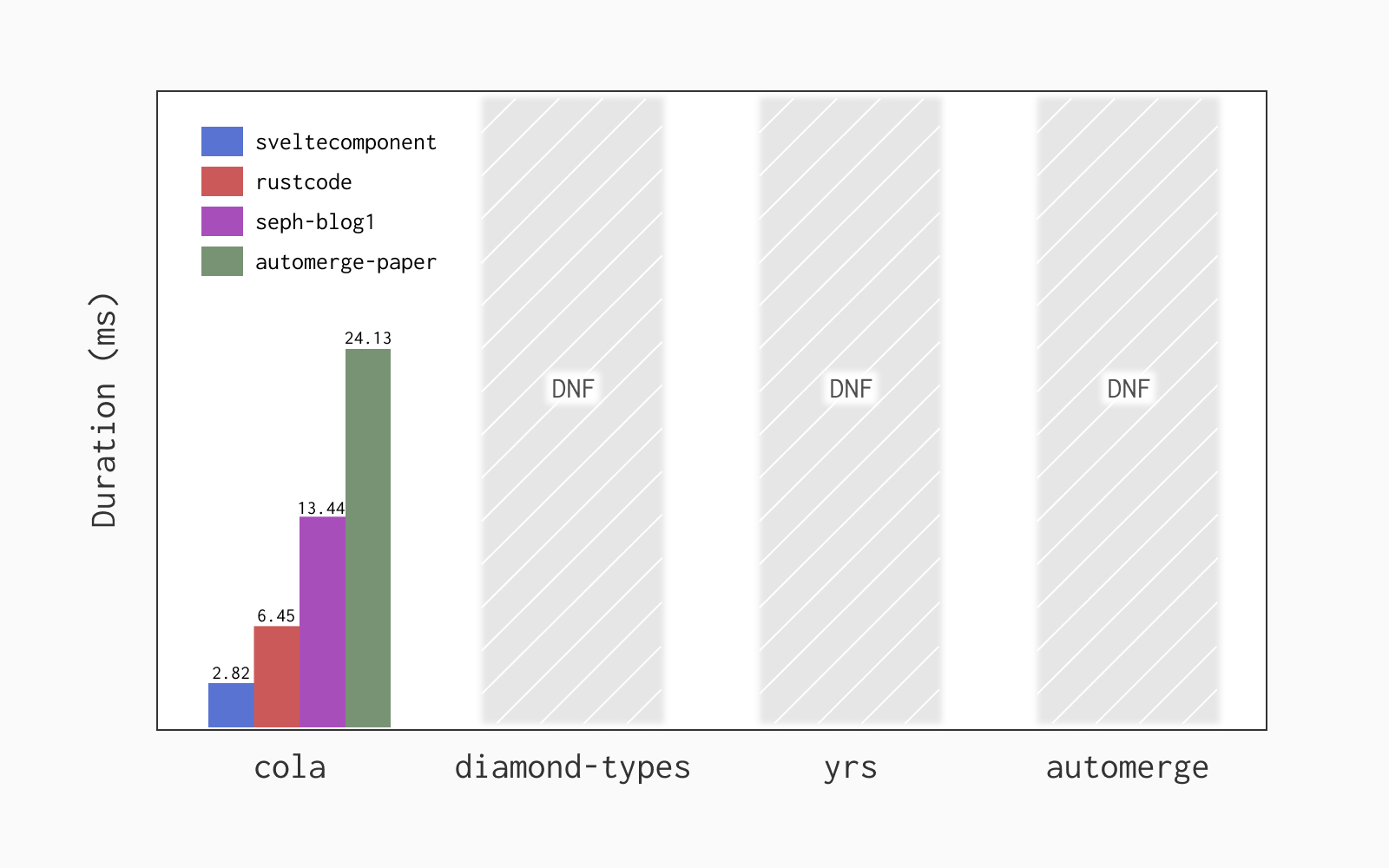
cola is ~2x slower than before, which is expected since integrating remote edits is in general more expensive than creating local ones, but it still performs amazingly well. It’s about as fast as (if not faster than) the fastest rope libraries in both directions, and it’s currently the fastest text CRDT implementation I know of.
✌🏻
-
this is not true if we want to support undoing deletions, which cola doesn’t do at the moment.↩︎
-
in cola this is called a version map instead of a version vector because, well, it’s shaped like a map and not like a vector.↩︎
-
just like in a B-tree, the inodes of a G-tree have a variable number of children. A branching factor of 32 means that every inode can have between 16 and 32 children, except for the root which can have as few as 2 children.↩︎
-
after processing the
automerge-paperediting trace cola’s G-tree has around ~15kEditRuns. And that trace is huge! It contains 260k edits and was recorded over several days.↩︎
